题目描述

关系

908-最大不相交区间数量
906-区间分组
112-雷达设备

内容

给定 $N$ 个闭区间 $[a_i,b_i]$，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式

第一行包含整数 $N$，表示区间数。

接下来 $N$ 行，每行包含两个整数 $a_i,b_i$，表示一个区间的两个端点。

输出格式

输出一个整数，表示所需的点的最小数量。

数据范围

$1\le N\le {10}^5$,
$-{10}^9\le a_i\le b_i\le {10}^9$

输入样例：

3
2 4
3 5

输出样例：

2

问题分析

最初思路

我们最多可以选 n 个点，所以设答案 res = n。
对左边界进行升序排序，对于任意一个区间 $[a_i,b_i]$，如果有一个区间 $[a_k,b_k]$，满足 $a_i\le a_k\le b_i$，那么我就让 res--，最后得出的答案就是 res。

思路分析

每个区间按照右端点从小到大排序。如果当前区间已经包含了点，就直接跳过，否则直接取右端点。因为右端点更有可能覆盖下一个区间。

证明

显然其他解一定是包含最优解的，所以 $B\le A$。
现在尝试证明 $A\le B$：

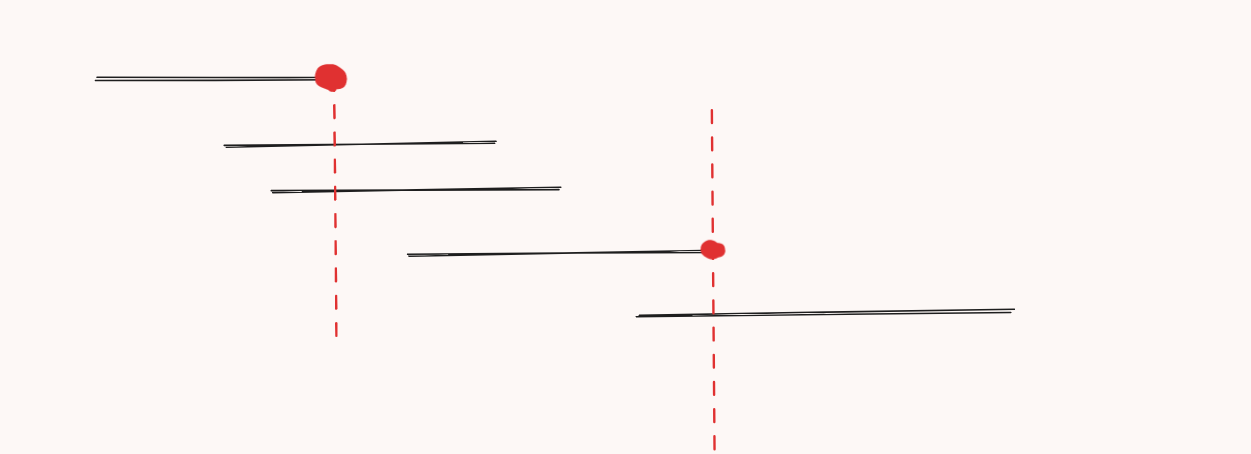
我们看看我们贪心选择的点有什么性质，先看下图：

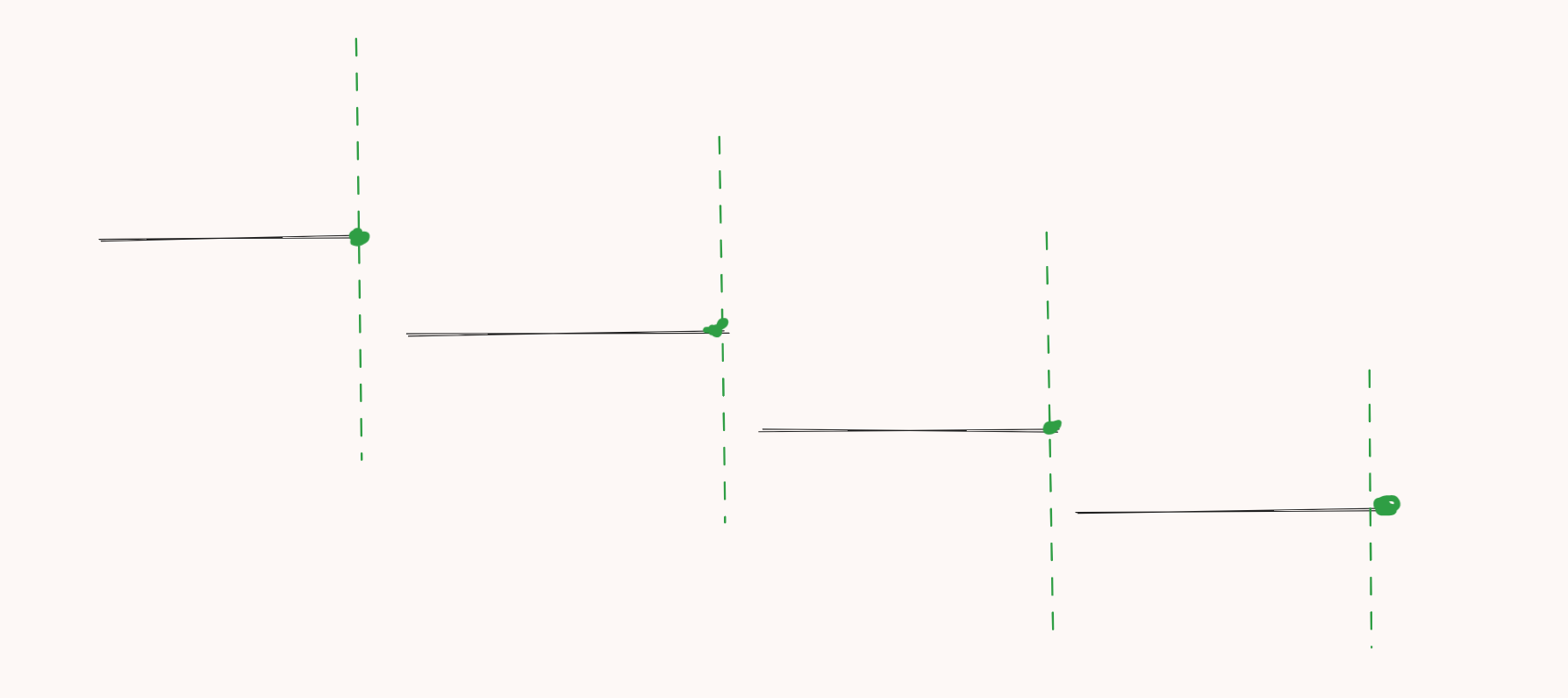
假如我们选择了一个区间的右端点，那么我们下一个选择的右端点所在的区间一定不与当前区间重合。而对于被我们选择右端点的区间（总量为 cnt），最优选择出来的区间也一定至少为 cnt 个。

也就是说，这 cnt 个区间，我最少放置 4 个点。这 cnt 个区间是主要矛盾，我们不可能花 3 个点覆盖 4 个不相交的区间。所以其余解的点的数量只能 ${\displaystyle \ge 4}$.

那么

故有 $A\le B$。从而 $A=B$。

证毕。

执行流程设计

总结

• 一般的区间问题都会去排个序，可以按左端点，也可以按照右端点排序；
• 区间的选择问题，主要矛盾在于其端点（两个端点唯一确定了一个区间）；
• 贪心的证明方法：证明集合相等（贪心选择出来的集合 $A$，和本来最优解的集合 $B$ 相等）：
  • $A\le B$；
  • $B\le A$；

代码实现

#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;

#define x first
#define y second

typedef pair< int , int > PII;


const int N = 1e5 + 10;

int n;
PII a[N];

bool cmp(PII a, PII b)
{
    return a.y < b.y;
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y;
    
    sort(a + 1, a + 1 + n, cmp);
    
    int res = n;
    for (int i = 1; i <= n; )
    {
        int j = i + 1;
        int r = a[i].y;
        while (j <= n && r >= a[j].x)
        {
            j ++;
            res --;
        }
        i = j;
    }
    cout << res;
    return 0;
}