题目描述

关系

内容

在游戏《星际争霸 II》中，高阶圣堂武士作为星灵的重要 AOE 单位，在游戏的中后期发挥着重要的作用，其技能”灵能风暴“可以消耗大量的灵能对一片区域内的敌军造成毁灭性的伤害。

经常用于对抗人类的生化部队和虫族的刺蛇飞龙等低血量单位。

你控制着 $n$ 名高阶圣堂武士，方便起见标为 $1,2,···,n$。

每名高阶圣堂武士需要一定的灵能来战斗，每个人有一个灵能值 $a_i$ 表示其拥有的灵能的多少（$a_i$ 非负表示这名高阶圣堂武士比在最佳状态下多余了 $a_i$ 点灵能，$a_i$ 为负则表示这名高阶圣堂武士还需要 $-a_i$ 点灵能才能到达最佳战斗状态）。

现在系统赋予了你的高阶圣堂武士一个能力，传递灵能，每次你可以选择一个 $i\in [2,n-1]$，若 $a_i\ge 0$ 则其两旁的高阶圣堂武士，也就是 $i-1、i+1$ 这两名高阶圣堂武士会从 $i$ 这名高阶圣堂武士这里各抽取 $a_i$ 点灵能；若 $a_i<0$ 则其两旁的高阶圣堂武士，也就是 $i-1,i+1$ 这两名高阶圣堂武士会给 $i$ 这名高阶圣堂武士 $-a_i$ 点灵能。

形式化来讲就是 $a_{i-1}+=a_i,a_{i+1}+=a_i,a_i-=2a_i$。

灵能是非常高效的作战工具，同时也非常危险且不稳定，一位高阶圣堂武士拥有的灵能过多或者过少都不好，定义一组高阶圣堂武士的不稳定度为 $ma{x}_{i=1}^n|a_i|$，请你通过不限次数的传递灵能操作使得你控制的这一组高阶圣堂武士的不稳定度最小。

输入格式

本题包含多组询问。输入的第一行包含一个正整数 $T$ 表示询问组数。

接下来依次输入每一组询问。

每组询问的第一行包含一个正整数 $n$，表示高阶圣堂武士的数量。

接下来一行包含 $n$ 个数 $a_1,a_2,···,a_n$。

输出格式

输出 $T$ 行。

每行一个整数依次表示每组询问的答案。

数据范围

$1\le T\le 3,3\le n\le 300000,|a_i|\le {10}^9$,
每个评测用例的限制如下：

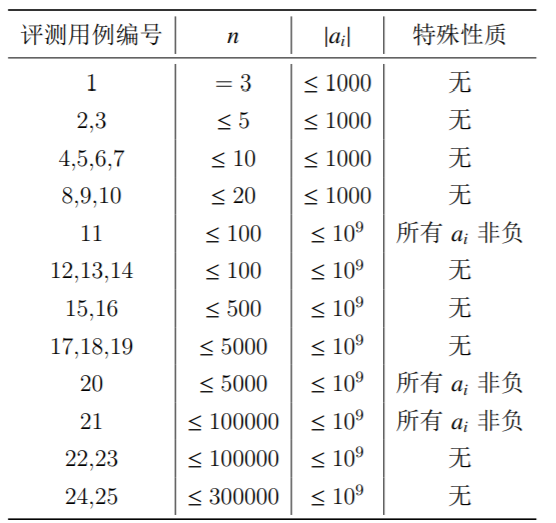
输入样例 1：

3
3
5 -2 3
4
0 0 0 0
3
1 2 3

输出样例 1：

3
0
3

输入样例 2：

3
4
-1 -2 -3 7
4
2 3 4 -8
5
-1 -1 6 -1 -1

输出样例 2：

5
7
4

样例解释

样例一
对于第一组询问：
对 $2$ 号高阶圣堂武士进行传输操作后 $a_1=3，a_2=2，a_3=1$。答案为 $3$。
对于第二组询问：
这一组高阶圣堂武士拥有的灵能都正好可以让他们达到最佳战斗状态。

问题分析

最初思路

思路分析

这道题具有一定的难度。
难点：

1. 用前缀和；

贪心我们常常要发现一个不变量，可以发现，我们不论如何进行操作，整个序列的总和一定是不变的。于是就有机会想到前缀和。

于是题目就转化为：
对 ${\displaystyle i\in [2,n-1]}$，我们可以交换 ${\displaystyle s[i],s[i-1]}$。现在要求一个最终的序列。使得 ${\displaystyle max(s[i]-s[i-1])}$ 最小。

很容器想到，如果 ${\displaystyle s}$ 是单调的，那么这种情况下，就是我们想要的情况。我们可以想象成一个楼梯。如果我们总是一会上一会下，那么会增加每一个台阶的高度差。

但是，麻烦的是我们无法操作 ${\displaystyle s[0],s[n]}$，也就是说我们只能能够通过交换行为保证 ${\displaystyle s[1]\to s[n-1]}$ 的单调性。

我们先将整个序列排一个序，然后从 ${\displaystyle s[0]}$ 开始走，如下图：

执行流程设计

1. 求前缀和数组 s。
2. 申请一个数组 f，用来存放最终的序列。

总结

代码实现

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

const int N = 3e5 + 10;
int t, n;
ll f[N];
bool st[N];
ll s[N];
ll a[N];

void solve() {
    // 预处理前缀和
    s[0] = 0;
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        s[i] += s[i - 1];
    }
    
    ll s0 = s[0], sn = s[n];
    if (s0 > sn) swap(s0, sn);
    
    sort(s, s + 1 + n);
    
    for (int i = 0; i <= n; i++) {
        if (s[i] == s0) {
            s0 = i;
            break;
        }
    }
    
    for (int i = 0; i <= n; i++) {
        if (s[i] == sn) {
            sn = i;
            break;
        }
    }
    
    memset(st, false, sizeof st);
    
    int l = 0, r = n;
    for (int i = s0; i >= 0; i -= 2) {
        f[l++] = s[i];
        st[i] = true;
    }
    
    for (int i = sn; i <= n; i += 2) {
        f[r--] = s[i];
        st[i] = true;
    }
    
    for (int i = 0; i <= n; i++) {
        if (!st[i]) {
            f[l++] = s[i];
        }
    }
    
    ll res = 0;
    for (int i = 1; i <= n; i++) res = max(res, abs(f[i] - f[i - 1]));
    printf("%lld\n", res);
}

int main()
{
    scanf("%d", &t);
    while (t--) {
        scanf("%d", &n);
        solve();
    }
    return 0;
}