有序表-sb 树
基本介绍
全名:sizeBalanceTree。
以叔叔节点为根的树的节点都不能比其侄子节点的节点要少。
eg. c 节点的节点个数要比 EF 都要多。
AVL 树中的平衡因子是高度,而 sb 树是节点个数。
不如 AVL 严苛,但是也可以维持平衡性。左右两树的高度差不会超过 2 倍。
一些约定
为了表示方便,我们用 tree 表示 sb 树,cur.left 表示以 cur 为根节点的左子树,cur.right 表示以 cur 为根节点的右子树。
用
平衡性的调整
与 AVL 树类似,就是平衡因子不同,AVL 树的平衡因子是高度,而 sb 树的平衡因子是节点数量。
AVL 树调整完后就不需要变化了,而 sb 树还需要进一步操作。当某些节点发生变化的时候,需要递归调用这些节点检查平衡性是否被破坏。检查所有受影响的节点。
为什么要这么检查?
因为在左旋和右旋操作过后,两树的节点可能会发生变化,所以需要重新判断。
为什么要递归调用?
LL 型
|cur.left.left| > |cur.right| :
对 cur 节点进行右旋。
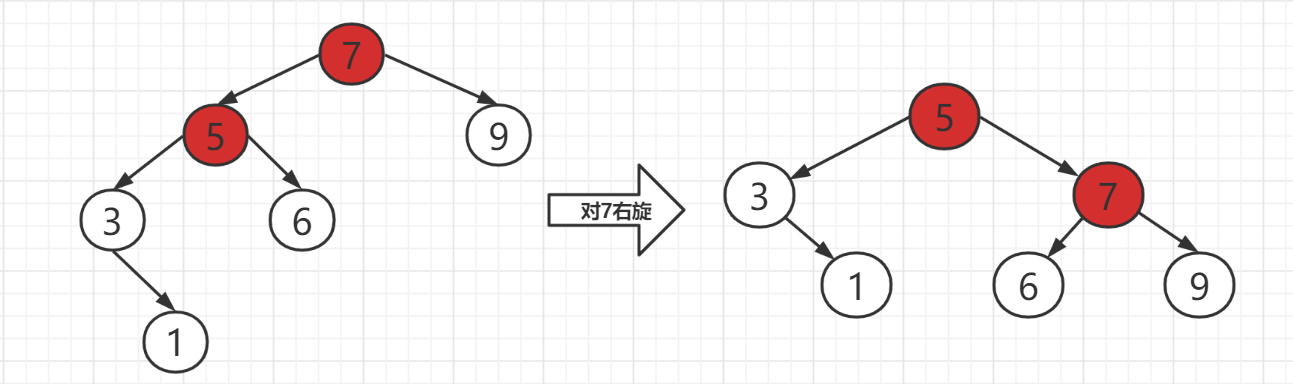
但是我们发现右旋过后,tree 虽然平衡了,但是 5 号节点和 7 号节点的节点发生了变化。也就是,可能会存在某种情况,使得右旋了之后仍然不平衡。
于是我们就需要对 5 、7 重新进行平衡性检查纠正。
总结可以得出我们需要对 cur 和 cur.right 重新进行平衡性调整。
LR 型
|cur.left.right| > |cur.right| :
对 cur.left 左旋,再对新的 cur.left 进行右旋。
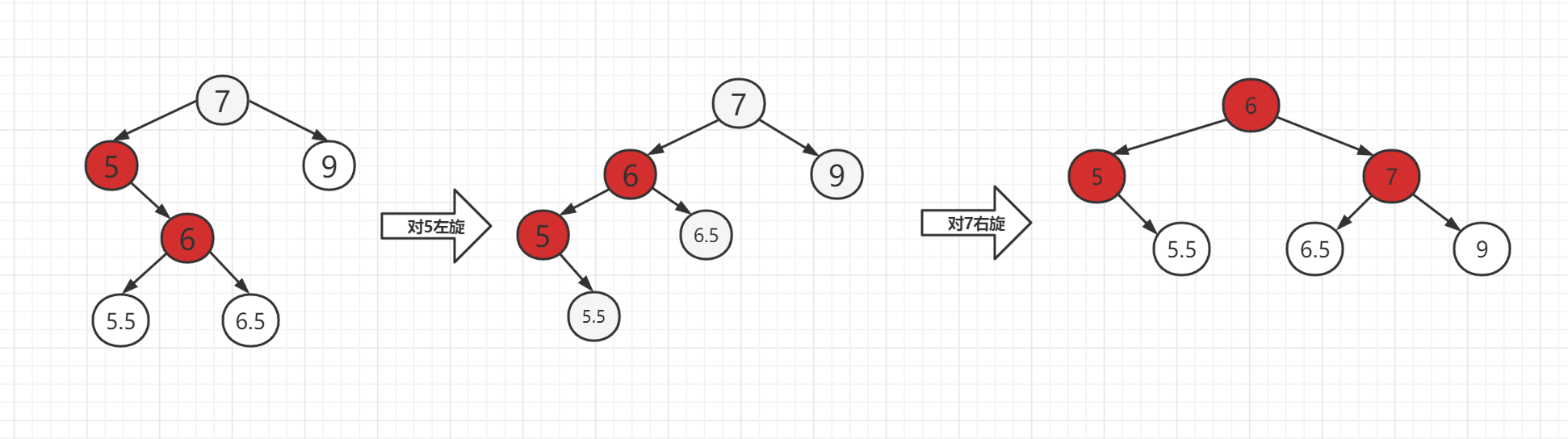
入上图,我们需要对 5 、6 、7 节点进行平衡性调整。
RR 型
cur.right.right| > |cur.left| :
对 cur 节点进行左旋。
平衡性调整策略与 LL 型对称。
RL 型
cur.right.left| > |cur.left :
对 cur.left 右旋,再对新的 cur.left 进行左旋。
平衡性调整策略与 LR 型对称。
基本操作
添加节点
删除节点
与 AVL 树类似也有三种情况,设待删除节点为cur:
- cur 没有左右孩子:直接删除。
- cur 只有左孩子:拿左孩子进行替换。
- cur 只有右孩子:拿右孩子进行替换。
- cur 左右孩子都有:拿右子树的最左节点进行替换,然后删除右子树的最左节点。
最后可以不用对 cur 节点进行平衡性检查。
优势
可以不在删除节点的时候检查平衡性,只在加入节点的时候调整。由于有了递归行为,所以依然可以调平。
代码实现
节点结构
public static class SBTNode<K extends Comparable<K>, V> {
public K key;
public V value;
public SBTNode<K, V> l;
public SBTNode<K, V> r;
/**
* 平衡因子,不同的key的数量
*/
public int size;
public SBTNode(K key, V value) {
this.key = key;
this.value = value;
size = 1;
}
}
树结构
private SBTNode<K, V> root;
/**
* 对cur进行右旋
*
* @param cur
* @return
*/private SBTNode<K, V> rightRotate(SBTNode<K, V> cur) {
SBTNode<K, V> leftNode = cur.l;
cur.l = leftNode.r;
leftNode.r = cur;
leftNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return leftNode;
}
/**
* 对cur进行左旋
*
* @param cur
* @return
*/private SBTNode<K, V> leftRotate(SBTNode<K, V> cur) {
SBTNode<K, V> rightNode = cur.r;
cur.r = rightNode.l;
rightNode.l = cur;
rightNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return rightNode;
}
平衡性调整
/**
* 对以cur为根节点的树进行平衡性调整
*
* @param cur
* @return
*/private SBTNode<K, V> maintain(SBTNode<K, V> cur) {
if (cur == null) {
return null;
}
int leftSize = cur.l != null ? cur.l.size : 0;
int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
int rightSize = cur.r != null ? cur.r.size : 0;
int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
//LL型
if (leftLeftSize > rightSize) {
cur = rightRotate(cur);
cur.r = maintain(cur.r);
cur = maintain(cur);
//LR型
} else if (leftRightSize > rightSize) {
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
//RR型
} else if (rightRightSize > leftSize) {
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur = maintain(cur);
//RL型
} else if (rightLeftSize > leftSize) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
}
return cur;
}
添加节点
/**
* 现在,以cur为头的树上,新增,加(key, value)这样的记录
* 加完之后,会对cur做检查,该调整调整
* 返回,调整完之后,整棵树的新头部
*
* @param cur
* @param key
* @param value
* @return
*/private SBTNode<K, V> add(SBTNode<K, V> cur, K key, V value) {
if (cur == null) {
return new SBTNode<K, V>(key, value);
} else {
cur.size++;
if (key.compareTo(cur.key) < 0) {
cur.l = add(cur.l, key, value);
} else {
cur.r = add(cur.r, key, value);
}
return maintain(cur);
}
}
/**
* 有序表 新增、改value
* key相同则替换
*
* @param key
* @param value
*/
public void put(K key, V value) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.key) == 0) {
lastNode.value = value;
} else {
root = add(root, key, value);
}
}
删除节点
public void remove(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
if (containsKey(key)) {
root = delete(root, key);
}
}
/**
* 在cur这棵树上,删掉key所代表的节点
* 返回cur这棵树的新头部
*
* @param cur
* @param key
* @return
*/private SBTNode<K, V> delete(SBTNode<K, V> cur, K key) {
cur.size--;
if (key.compareTo(cur.key) > 0) {
cur.r = delete(cur.r, key);
} else if (key.compareTo(cur.key) < 0) {
cur.l = delete(cur.l, key);
//要删除cur
} else {
//没有孩子
if (cur.l == null && cur.r == null) {
cur = null;
//只有右
} else if (cur.l == null && cur.r != null) {
//拿右节点替换
cur = cur.r;
//只有左
} else if (cur.l != null && cur.r == null) {
//拿左节点替换
cur = cur.l;
// 有左有右
} else {
SBTNode<K, V> pre = null;
//des初始化为右树根节点
SBTNode<K, V> des = cur.r;
des.size--;
//找到右树的最左节点
while (des.l != null) {
pre = des;
des = des.l;
//沿途将所有的size减小1
des.size--;
}
//此时des指向右树的最左节点,pre为des的父节点
if (pre != null) {
pre.l = des.r;
des.r = cur.r;
}
des.l = cur.l;
des.size = des.l.size + (des.r == null ? 0 : des.r.size) + 1;
// free cur memory -> C++
cur = des;
}
}
//这里可以不用对cur节点进行平衡性检查
cur = maintain(cur);
return cur;
}
改写技巧
我们在使用有序表的时候时常使用 sb 树进行定制化。