AVL 树基本介绍

具有最严苛的平衡性。任何一个节点，其左树与右树的高度差不超过 1，即小于 2 。
AVL 在加入和删除节点时与搜索二叉树相同，但在节点操作之后要进行相应的平衡操作。
搜索二叉树如何删除节点？找到待删除节点的右子树的最左节点（左树上的最右节点也行）来替换这个节点。

基本术语

平衡因子（平衡度）：即左子树的高度减去右子树的高度。

AVL 树的平衡性破坏原因

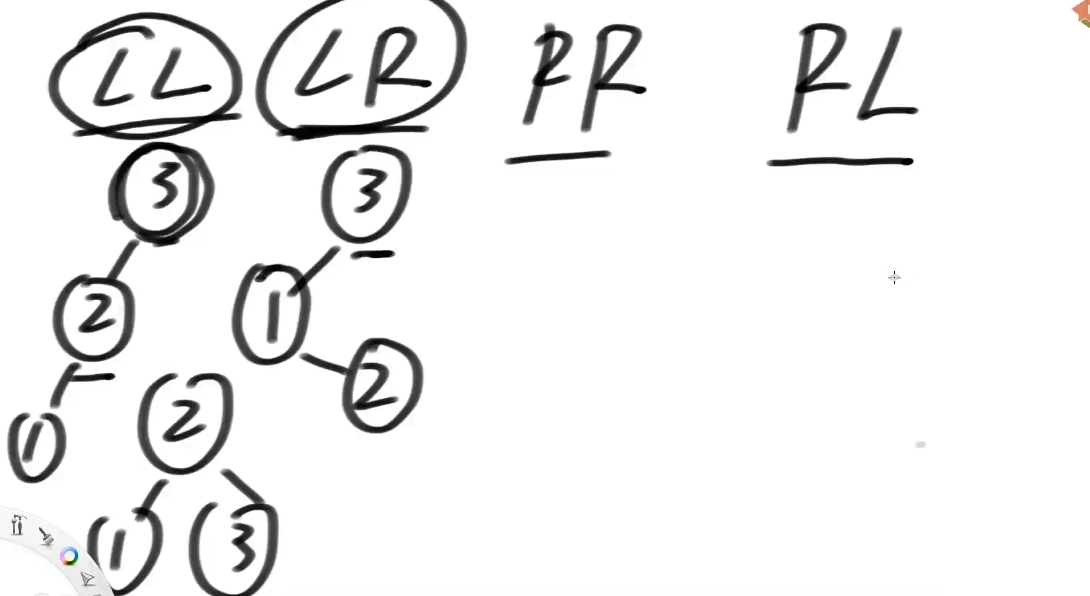
LL 型

即左子树的左子树过长导致高度差过大。只做一次右旋即可；

LR 型

左子树的右子树过长导致平衡性破坏。想办法让这个右子树（孙子）来到头节点的位置。先以左子树为头进行左旋，再对旋转上来的右子树（原来的孙子，现在成了儿子）为头进行右旋；

RR 型

同理，做一次左旋即可；

RL 型

同理。想办法让这个左子树（孙子）来到头节点的位置。先以右子树为头进行左旋，再对旋转上来的左子树（原来的孙子，现在成了儿子）为头进行左旋；

LL+LR 型

怎么理解？看例子。按照 LL 型进行调整，默认其为 LL 型；
实例：

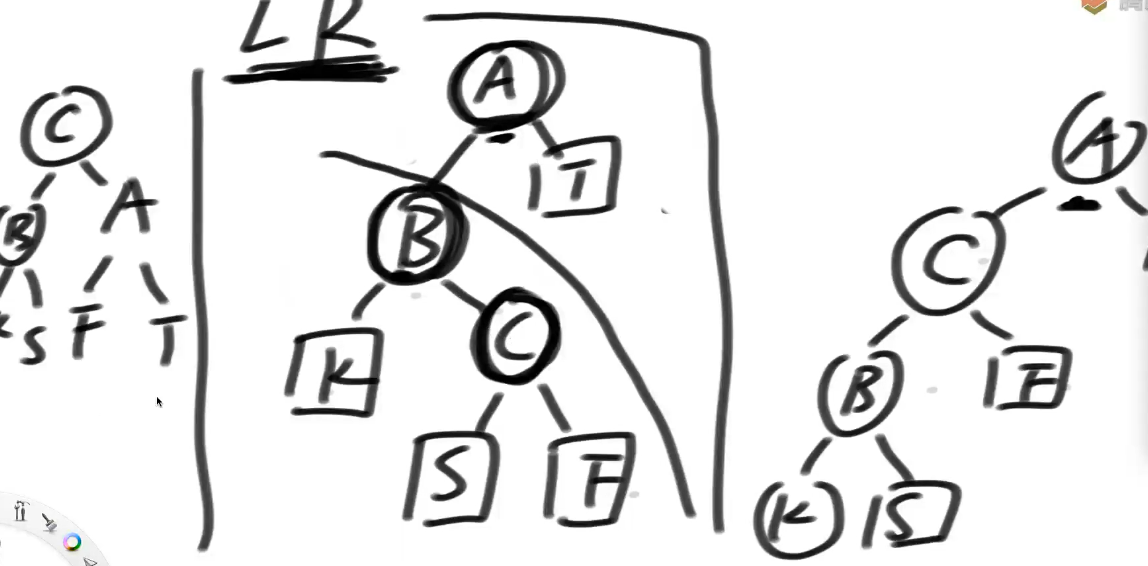
LL 型和 LR 型：

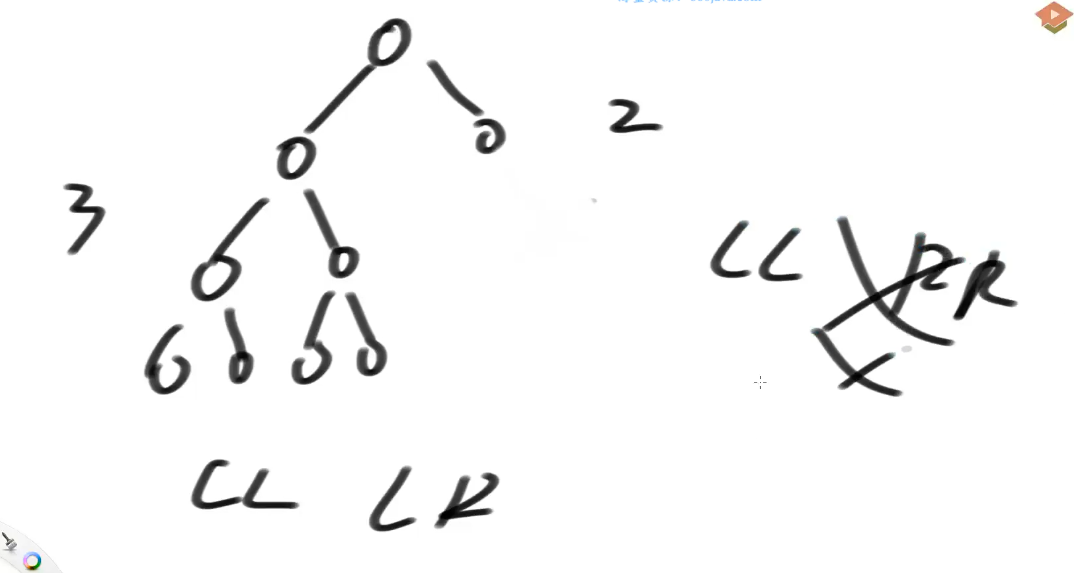
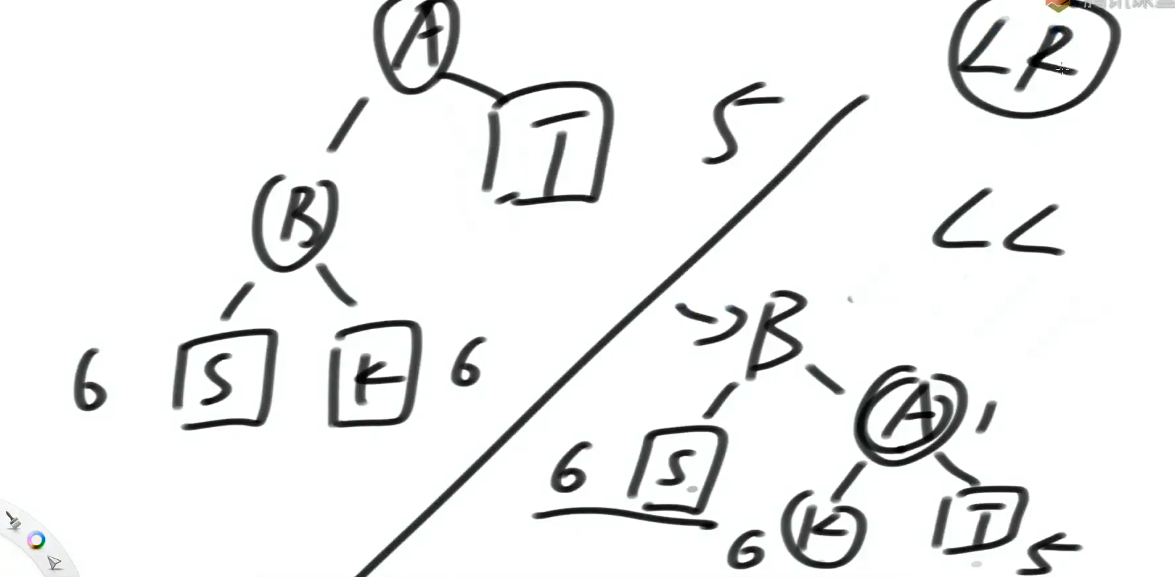
AVL 树加入删除操作后如何检查平衡性：

• 加入节点。当加入节点成功之后，从这个节点开始往上每一个节点都查一遍——查父亲，查爷爷，查太爷爷，查……直到发现不平衡或者遍历到头了。这种调整的最差时间复杂度为 $O(logN)$；
• 删除节点：
  1. 当这个待删除节点没有左右孩子的时候，与加入节点的检查相同；
  2. 只有右孩子，那就以这个被替换上来的右孩子向上查；
  3. 既有左孩子，又有右孩子。以这个被替换上来的右孩子原来的位置向上查；
     删除节点实例：
     
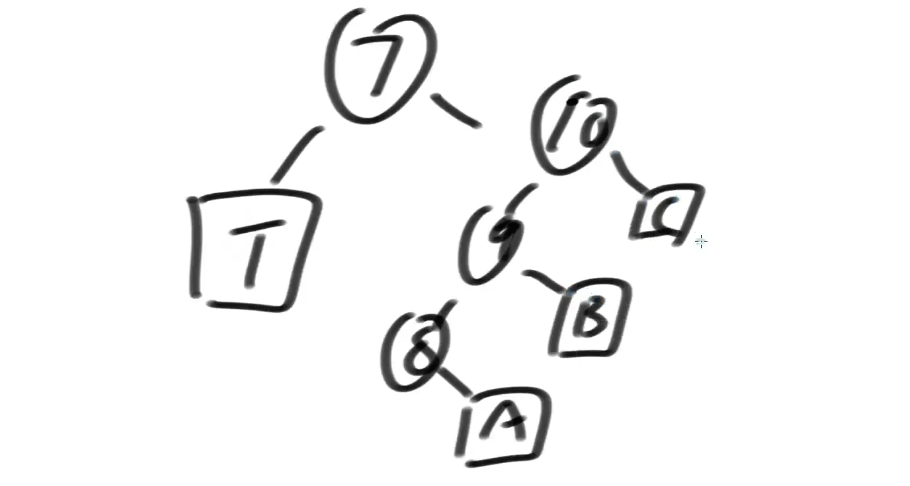
     假设要删除 7，那么就以 8 替换这个 7，于是变成了：
     
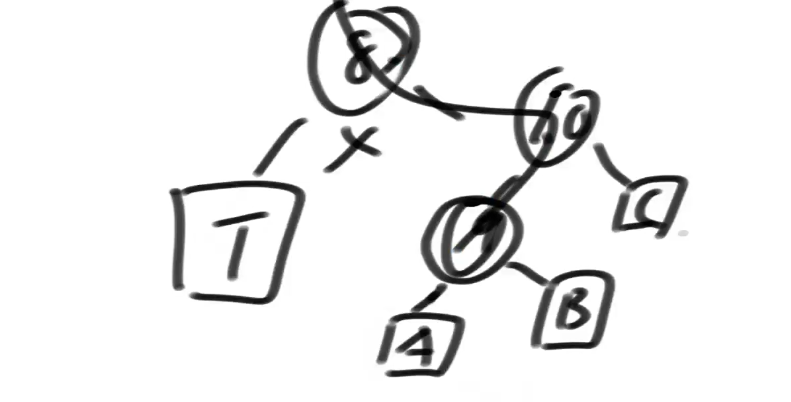
     从 9 开始